Proof Of Afterlife By Geometry

5.4 Section Four – Inverse Relationship

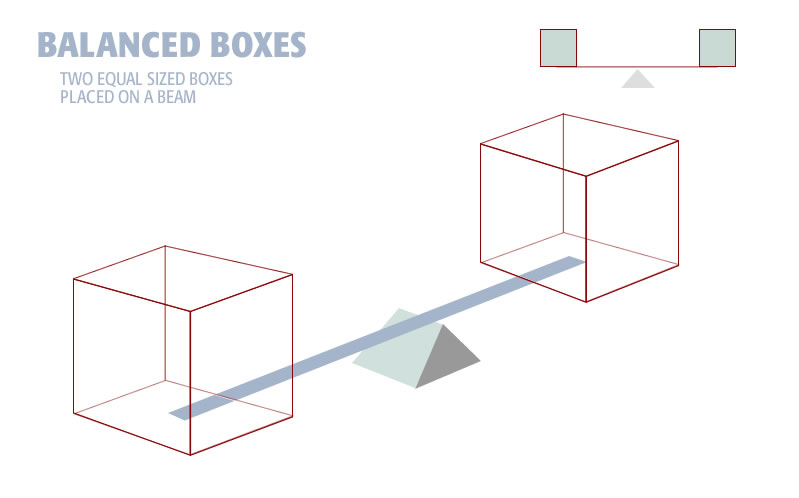
5.4.1 Equal Boxes in Balance

As we made the inner box smaller, the outer box became correspondingly larger. The reason the boxes reacted like this is because they are inverses of each other. To understand what that means take the boxes off the pyramid and place them on a balance beam. Here we show the two boxes, exactly the same size, as we initially set them on the balance beam:

The primary condition is that the system remain in balance. In the drawing above the boxes are the same size and are the same distance from the fulcrum. Thus the system is in balance.

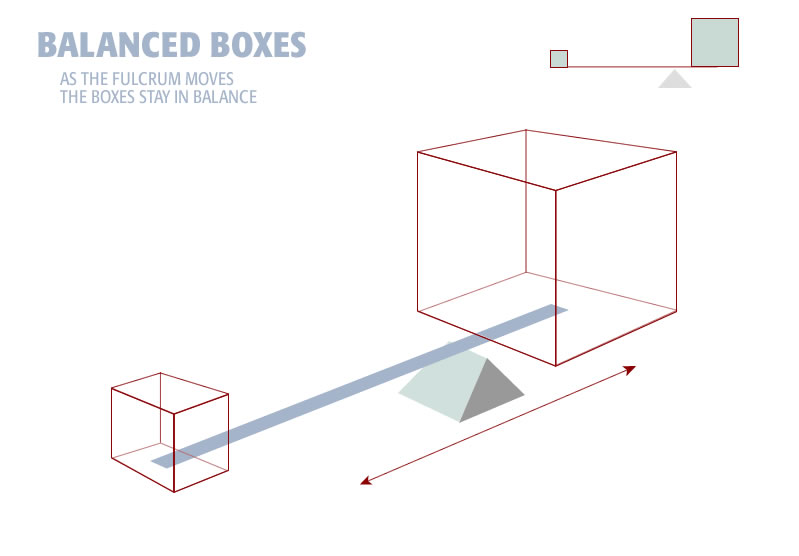
5.4.2 Unequal Boxes in Balance

In the drawing below we move the fulcrum away from the center toward one of the boxes. Because the system must remain in balance one box becomes larger and the other box becomes correspondingly smaller.

I have presented the last two diagrams so you can “feel” the inverse relationship. The important thing is balance of the system. That must be maintained. The boxes in the system adjust accordingly to maintain balance. When you adjust one side of the system, the other side adjusts accordingly.

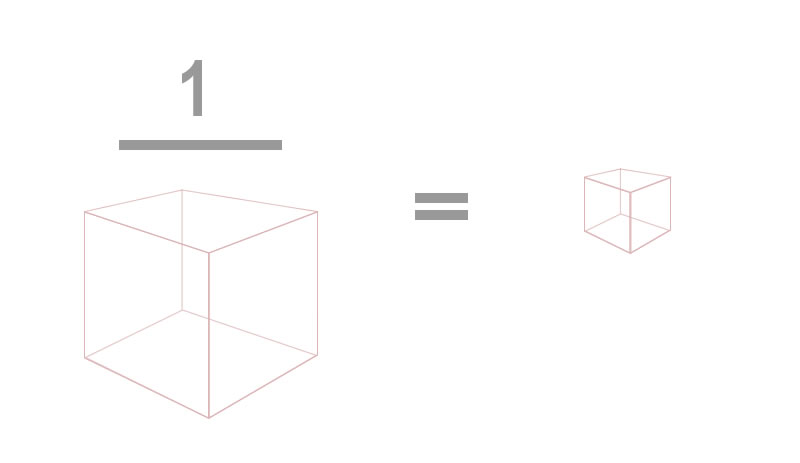
5.4.3 Inverse Expressed As An Equation

Here are the two boxes expressed as an equation. For the equation to hold, as the left box gets larger, the right box must get smaller.

An inverse relationship means as one box gets smaller the other box gets larger. Initially the volume of each box is one cubic unit. Each side is equal. If you increase the size of the left box by two, the corresponding box on the right must decrease by one half. This way the two boxes to maintain their inverse relationship. The equation holds true always. The elements within the adjust adjust themselves, doing what is necessary to keep the system in balance.

With an understanding of the underlying inverse relationship between the two boxes we are now going to place them back on the pyramid.

Proof Of Afterlife By Geometry – Section Five – Awareness And Memory